いろいろ 三角形 相似 条件 300196-三角形 合同 相似 条���

 一、相似三角形的判定定理： 1平行于三角形一边的直线和其他两边和两边的延长线相交，所构成的三角形与原三角形相似。 2如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。 3如果一个三角形的三条边三角形 ABC A B C と三角形 DEF D E F が相似ならば、 3 3 つの辺がすべて同じ倍率で縮小（拡大）されているわけです。 つまり、合同条件では「辺の長さが等しい」だった箇所が、相似条件では「辺の比が等しい」になっています。 ①3組の辺の比が等しい 合同条件では、「 3 3 つの辺がそれぞれ等しい」でした。 それはつまり、長さが a a, b b, c c の 3 3 本の棒を P P くんと Q Q くんのそれぞれ 2つの三角形が合同かどうかを判断するには、すべての辺や角を調べなくても、ある条件を満たせば、合同であることがいえます。 この条件のことを、 三角形の合同条件 といいます。 また、2つの図形が合同であることを式で表すときは、合同を表す「≡

三角形相似条件 证明 Doc 皮匠网

三角形 合同 相似 条件

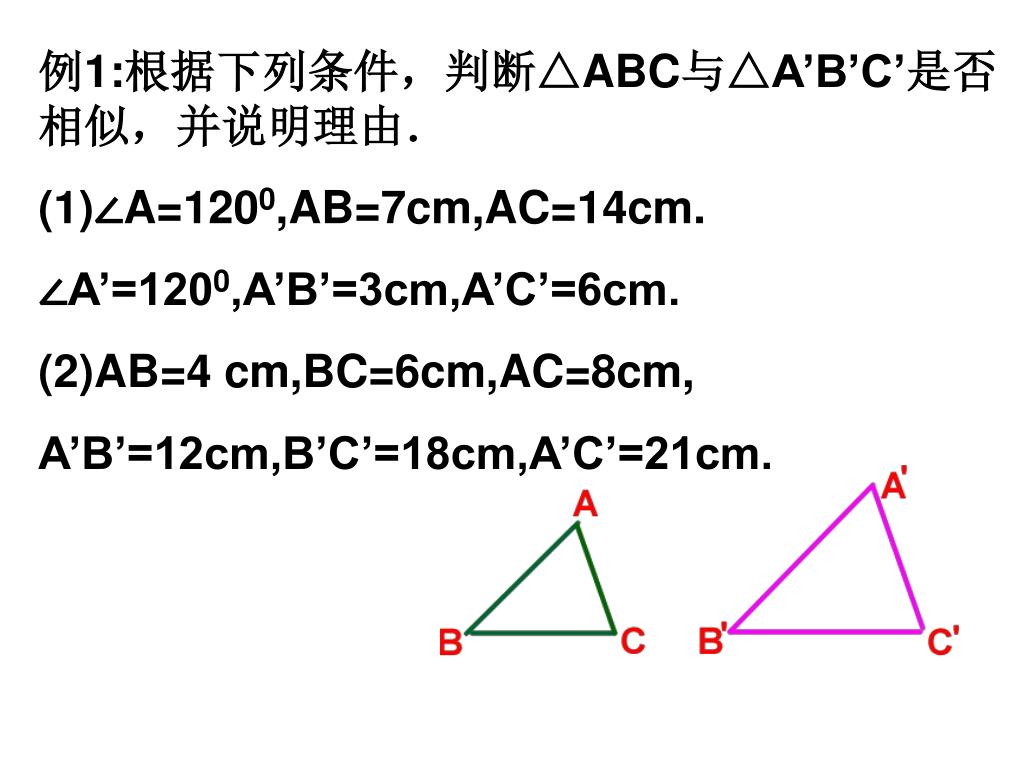
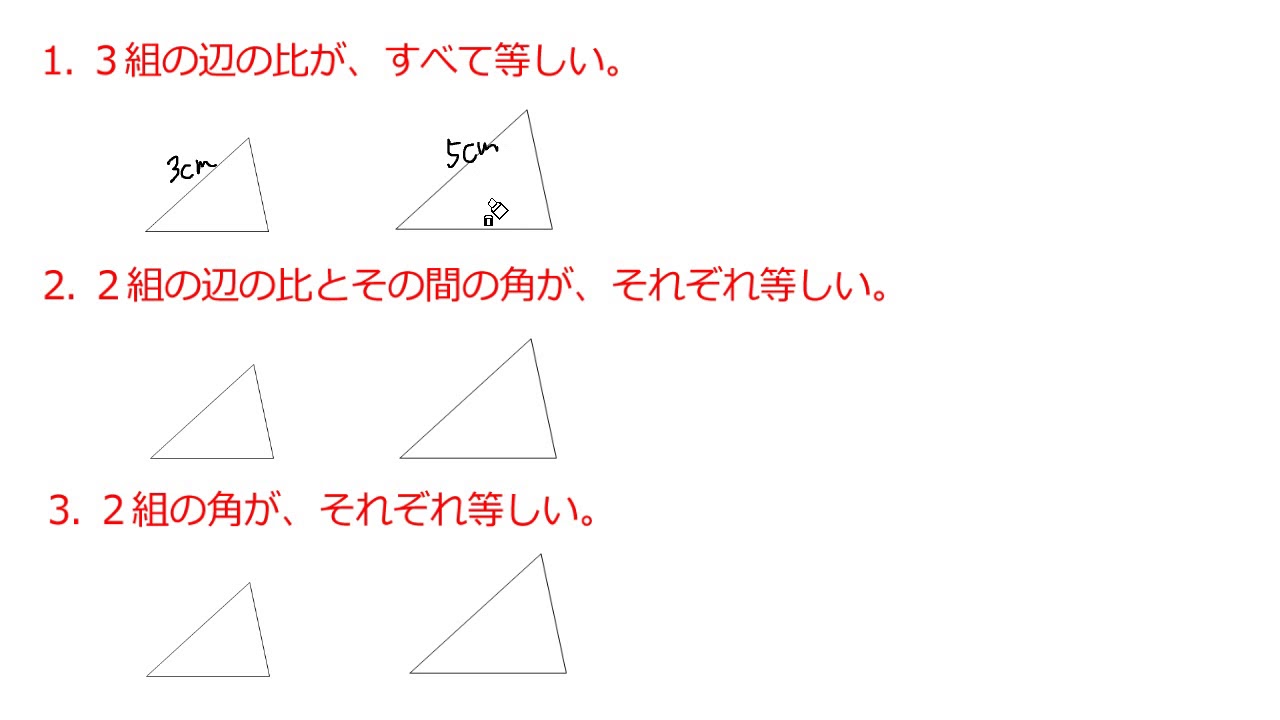
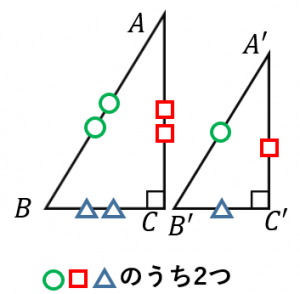
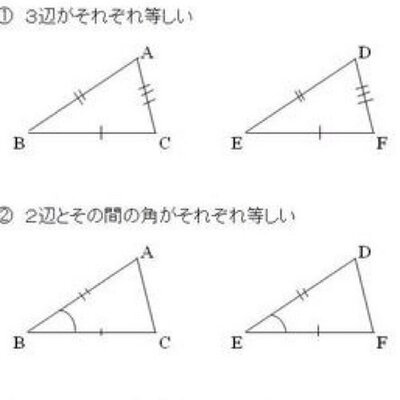
三角形 合同 相似 条件-三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき 3 2組の角が、それぞれ等しいとき 浙教版数学九年级上册：44 第1课时 三角形相似的预备定理和判定定理1（利用两角关系） 同步课件（22张ppt） 浙教版数学九年级上册同步课件：44 第3课时 相似三角形的判定定理3(共22张PPT) 浙教版九年级上册 44 两个三角形相似的判定 教案（3课时，表格式）

初中数学4 探索三角形相似的条件图片ppt课件 教习网 课件下载

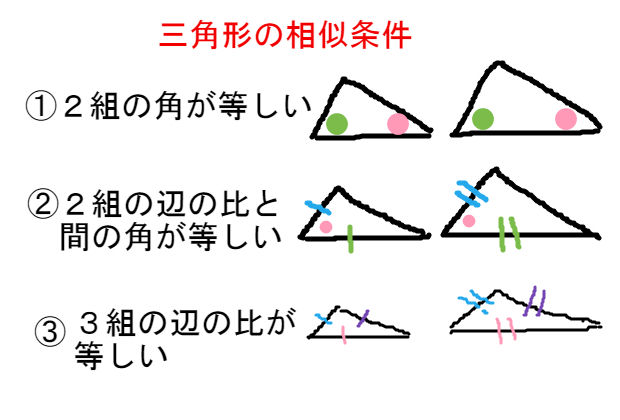
 三角形の相似条件 ① 組の辺の比がそれぞれ等しい ② 組の辺の比とその間の角が等しい ③ 組の角がそれぞれ等しい 三角形の相似条件は、相似を証明する問題ではもちろん、辺の長さや角度を求める問題でも利用することがあります。 合同条件と似ていますが、辺についてはあくまでも「比」が等しいという点に注意しましょう。 それぞれの相似条件を詳しく見てみましょう。 ① 3 組の辺三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」が 三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。 3つの何かが等しい条件 2つの角が等しい条件 2つの辺を角が挟んでいる条件 種類1 「3つの何かが等しい条件」 まず1つ目の条件の種類は、 3つの「何か」が等しいやつ だ。 合同条件と相似条件をそれぞれ見ていこっか。 合同条件1「3つの辺の長さがそれぞれ等しい」 「3つの辺の長さ」 がすべて等し

第5章 図形と相似 ＜前： L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答 ：次＞ 練習問題1 以下の1～3に示した各組の三角形が相似であることを証明しなさい。 （※辺の長さの単位はcm） 1 ABCと EDC 2 ABCと AED 3 ABCと EBD以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これら直角三角形の相似条件 直角三角形の相似条件1（よく使う、重要）： 直角以外の角度一つが等しい。 つまり、 ∠ A = ∠ A ′ または ∠ B = ∠ B ′ 直角三角形の相似条件2（めったに使わない）： 対応する2辺の比が等しい。 つまり、

情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている abcと abdが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめこんにちは、ウチダです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しまし三角形の相似条件 中学3年では，主に三角形の相似について学習します。2組の三角形があるとして，以下に挙げる3つの条件のうち，どれか1つが当てはまれば，その2組の三角形は相似といえます。 abcと defが相似の場合， abc∽ defと表します。

判断两个直角三角形相似的条件 网圈部落

数学4 3 相似三角形达标测试 教习网 试卷下载

 两个三角形相似的条件 文/张孟影 (1)平行于三角形一边的直线和其他两边和两边的延长线相交，所构成的三角形与原三角形相似；(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。 相似条件と合同条件の違いとは？ 18年7月24日 2つの三角形が合同であることを示すための条件を、 三角形の合同条件 と言います。 以下の3つの合同条件のうち、 どれか1つでも成り立っている なら「それらの三角形は合同である」ということができます 重点：探究三角形相似的方法 难点：对全等三角形条件的弱化过程。 学习目标： 1类比相似多边形，定义相似三角形，并能利用定义解决简单问题。 2类比三角形全等条件，猜想三角形相似条件，领悟类比思想方法，发 展合情推理能力和逻辑推理意识。 3

相似三角形判定定理 数学定理 搜狗百科

第4章图形的相似4探索三角形相似的条件第3课时相似三角形的判定 Ppt 师客文库

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru下図において、 ABCと相似な三角形をすべて見つけ、記号を使って表し、相似条件も答えなさい。 ＜前：L29 相似な図形とその性質 の問題 L30 三角形の相似条件 の解答：次＞  中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧3つの直角三角形はすべて相似ですから、下図のような辺の比になります。 51cmは、比⑰になりますから、比①＝3cm です。 比④＝12cm ですから、この直角三角形の面積は 51 × 12 ÷ 2 ＝306 正方形4つ分の面積は、この直角三角形の2倍ですから 306 × 2 ＝ 612 です

判断两个直角三角形相似的条件 网圈部落

4 4 1 探索三角形相似的条件1 新北师大版 Ppt 八斗知识文库

 2223学年北师大版九年级数学上册《44探索三角形相似的条件》 同步达标测试题（附答案） 一．选择题（共8小题，满分32分） 1．下列各组图形可能不相似的是（ ） a．有一个角是60°的两个等腰三角形 b．各有一个角是45°的两个等腰三角形 c．各有一个角是105°的两个等腰三角形 两角对应相等，两个三角形相似；两边对应成比例且夹角相等，两个三角形相似；三边对应成比例，两个三角形相似；三边对应平行，两个三角形相似；斜边与直角边对应成比例，两个直角三角形相似；全等三角形相似。 1如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。 (简叙为：两角对应相等，两个三角形相似。 ) 2如果两个三角形的两组对应边成比例， 1、两个角对应相等的三角形相似。 2、三边对应成比例的三角形相似。 3、两边对应成比例一个角对应相等的三角形相似。 94 评论 (3) 分享 举报 unique_loy TA获得超过1745个赞 关注 对应脚度相同，对应边成比例 26 评论 分享 举报 裴依邓晔晔 TA获得超过3638个赞 关注 三角形相似的判定定理如下： 1）角角即两个角对应相等即可 2）边角边即两个边对应成比

探索三角形相似的条件 相似图形ppt课件2下载 牛二ppt

掌握这些方法 初中数学相似三角形全等三角形证明题都能得满分 初中数学 学习资料大全 免费学习资源下载

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru四、三角形相似的证题思路：判定两个三角形相似思路： 1）先找两对内角对应相等 (对平行线型找平行线)，因为这个条件最简单； 2）再而先找一对内角对应相等，且看夹角的两边是否对应成比例； 3）若无对应角相等，则只考虑三组对应边是否成比例； 五证明三角形相似有三种方法： （1）两三角形中有两组角对应相等 （2）两三角形中有一组角对应相等,夹这两个相等角的两组边对应成比例 （3）两三角形三组边都对应成比例 解析看不懂？ 免费查看同类题视频解析 查看解答 更多答案 (2)

27 2 相似三角形 人教版九年级下册数学电子课本 数九网

Ppt 三个角对应 三条边对应 的两个三角形 叫做相似三角形powerpoint Presentation Id

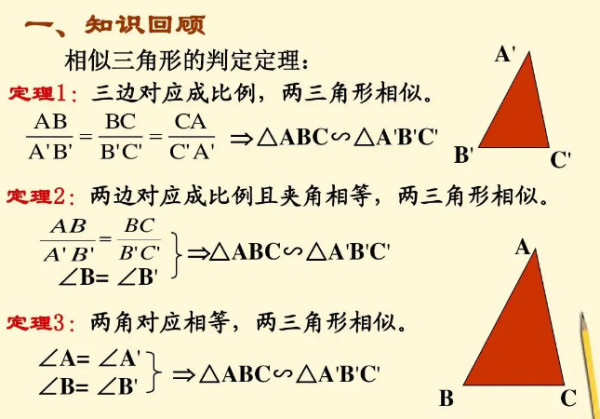
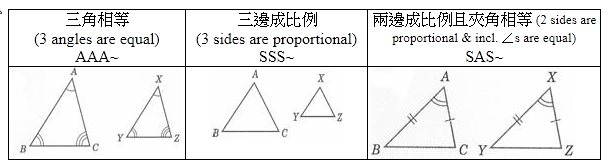
相似三角形的判定 类比全等三角形的判定定理，可以得出下列结论： 定理 两角分别对应相等的两个三角形相似。 定理 两边成比例且夹角相等的两个三角形相似。 定理 三边成比例的两个三角形相似。 定理 一条直角边与斜边成比例的两个直角三角形相似。 根据以上判定定理，可以推出下列结论： 推论 三边对应平行的两个三角形相似。 1 推论 一个三角形的两边和三角形任意一边上的中线与另一个三角形的对三角形の合同条件を思い出す。 本時の学習内容「2つの三角形が相似になる条件を調べよう」を知る。 課題を考える。 ABCと線分EFがあります。 BC：EF＝1：2のとき、 DEFとなる DEFをかきましょう。 対応する辺がすべて1：2となることを確認する。 DEFを（2）如果两个三角形对应边的比相等且夹角相等,这2个三角形也可以说明相似（简叙为： 两边对应成比例且夹角相等，两个三角形相似 ）； （3）如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似（简叙为 三边对应成比例，两个三角形相似 ）； （4）如果两个三角形的 两个角分别对应相等 （或三个角分别对应相等），则有两个三角形相似（简叙为 两角对应相等，两个

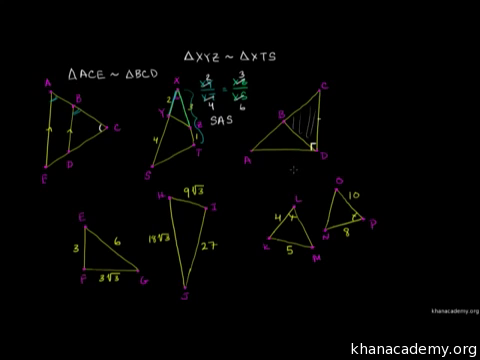
证明相似三角形 视频 三角形相似的定义 可汗学院

三角形の相似条件と証明問題の解き方 数学fun

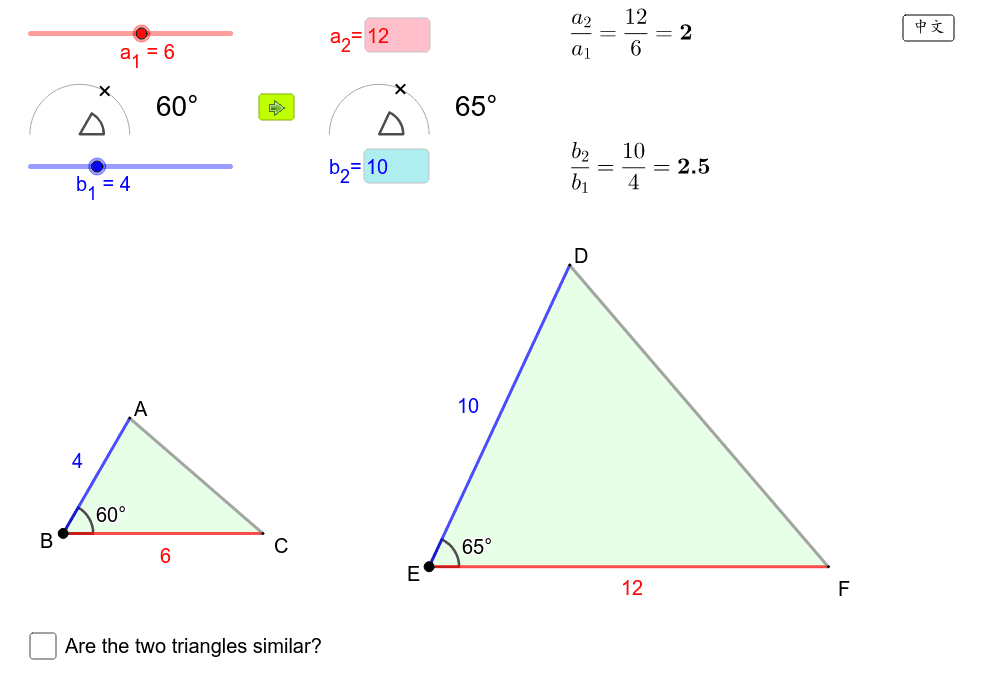
 1、三角形相似的判定方法 ①、定义法：对应角相等，对应边成比例的两个三角形相似 ②、平行法：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似 ③、判定定理1：如果一个三角形的两个角与另一个三角形的问题2类比三角形全等的判定方法（SAS,SSS），猜 想可以添加什么条件来判定两个三角形相似？ f想一想 ？ 如果 ABC与 A'B'C'两边成比例，且其中一边 所对的角相等，那么这两个三角形直角三角形, 二等辺三角形, ひし形, 長方形, 楕円, 双曲線, 角柱, 角錐, 円柱, 円錐など 適当な条件を加えると、それぞれ相似になる。 特に三角形においては、後述するように、相似となるための必要十分条件がよく知られている。 相似比

探索三角形相似的条件 相似图形ppt课件6下载 牛二ppt

探索三角形相似的条件 相似图形ppt课件2下载 牛二ppt

 三角形の相似条件 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99％「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。 四角形に対角線をひいてください。 対角線の交点は四角形の中心を通ります。 つまり、これは同じ長さの底辺から 2つの角が等しい三角形がかけたことになります。 あとは、底辺に対して水平に線をひいても 大きさは違えど角度が同じ相似な三角形が

相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt

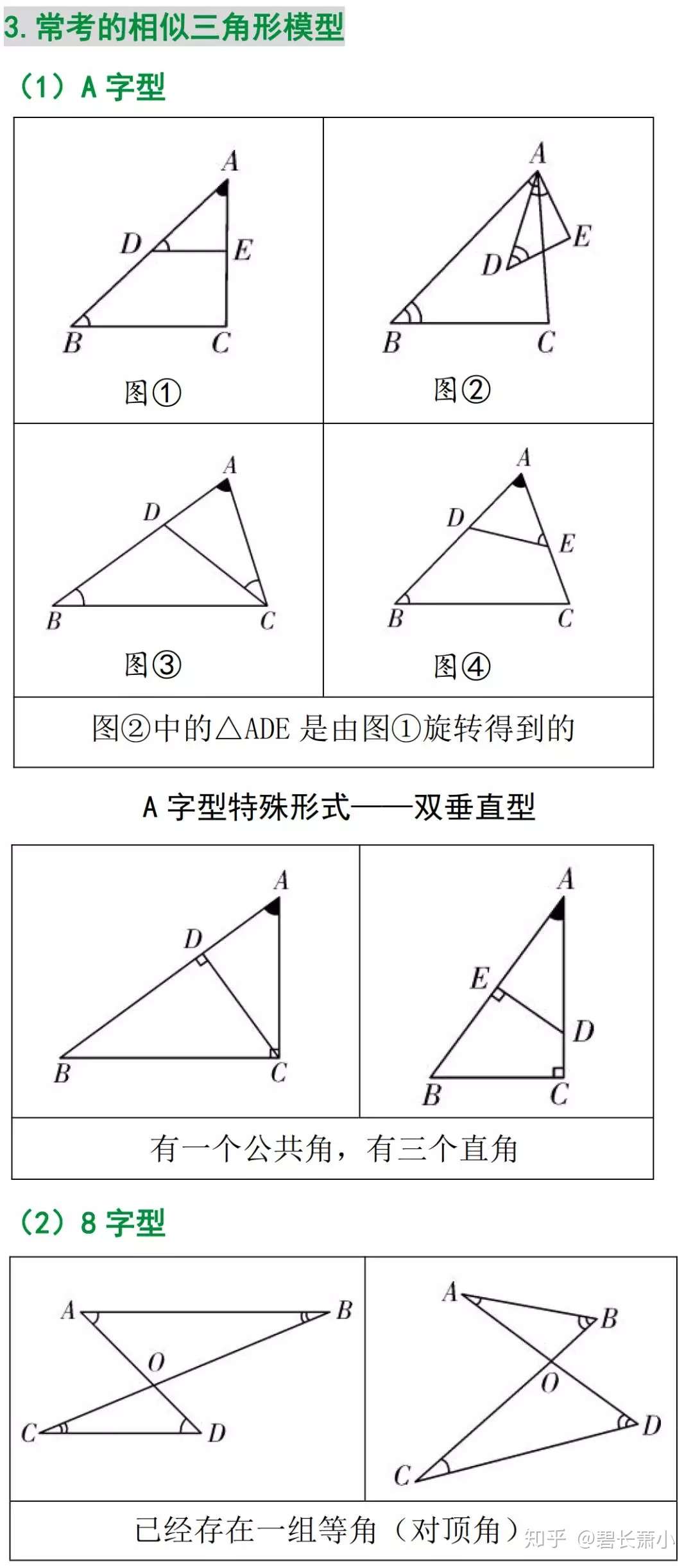
中考数学 相似三角形有关的证明与计算 知乎

4 5 1相似三角形判定定理的证明 哔哩哔哩 つロ干杯 Bilibili

Studydoctor三角形の相似条件 中３数学 Studydoctor

初中数学4 探索三角形相似的条件图片ppt课件 教习网 课件下载

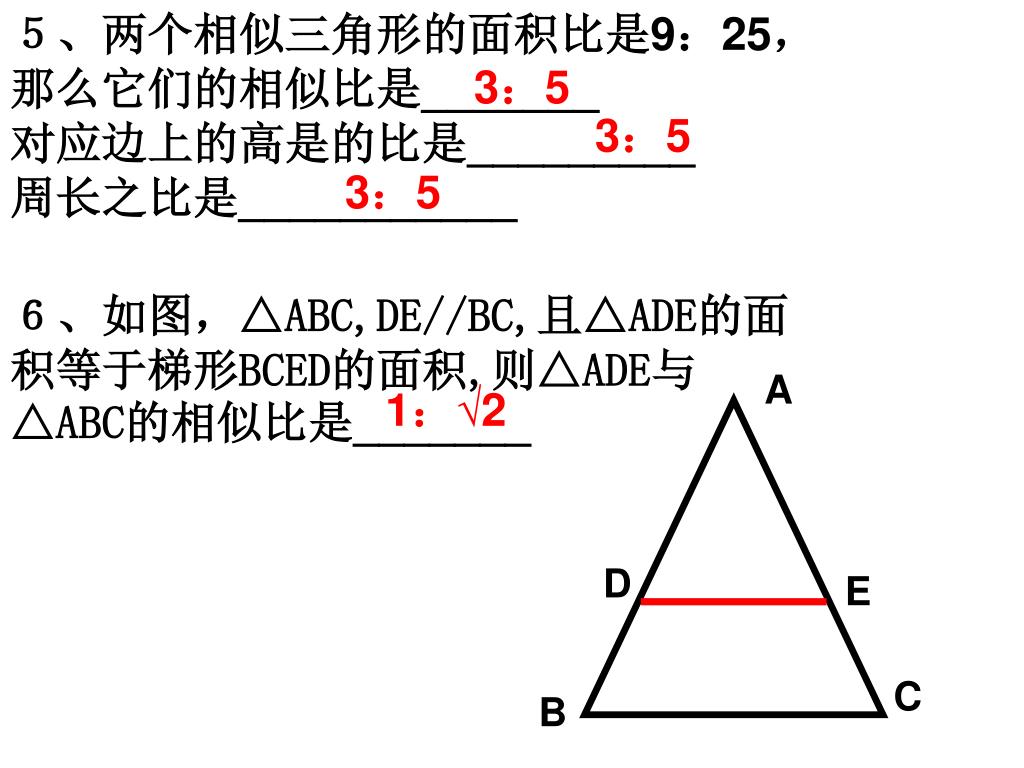
Ppt 27 2 ３相似三角形的周长与面积powerpoint Presentation Id

掌握这些方法 初中数学相似三角形全等三角形证明题都能得满分 初中数学 学习资料大全 免费学习资源下载

08全等三角形的判定 Hl 三角形的证明初中数学初二 Youtube

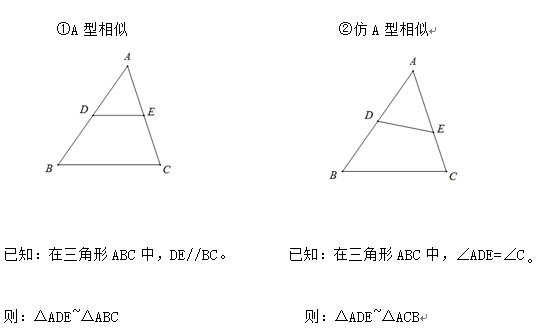
初中数学知识点相似三角形的判定及性质

3 Png

探索三角形相似的条件 图形的相似ppt 第3课时 第一ppt

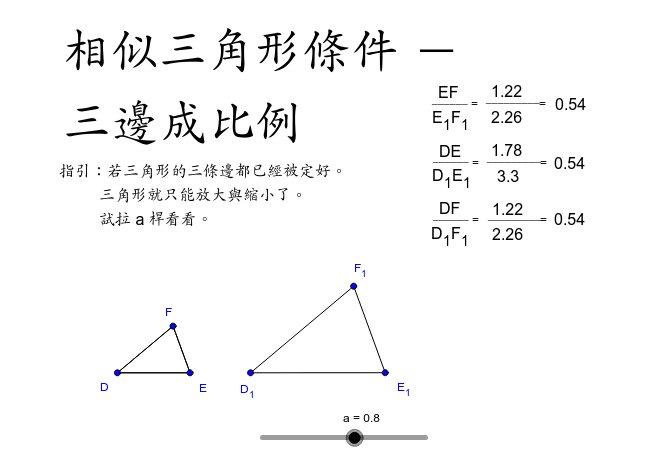
相似三角形條件 三邊成比例 Geogebra

专题27 11 相似三角形的判定 基础篇 专项练习 21 22学年九年级数学下册基础知识专项讲练 人教版 Docx 师客文库

判断两个直角三角形相似的条件 网圈部落

相似 几何 Wikiwand

三角形相似性复习 文章 三角形相似的定义 可汗学院

解读相似三角形经典图形 参考网

1

北师大4 4 1 探索三角形相似的条件 1 Ppt

突破难点的关键是构造直角三角形相似基本型 图形

探索三角形相似的条件 图形的相似ppt课件 Ppt课件下载 人人ppt

初中数学4 探索三角形相似的条件课后测评 教习网 试卷下载

初中数学相似三角形八种模型中文版你收藏了吗 Ren Ren School Buddy Facebook

Css3 三角形 初中数学 相似三角形模型合集提分收藏 爱代码爱编程

相似三角形 三角分別相等 三邊成比例的兩個三角形叫做相似三角形 Simi 百科知識中文網

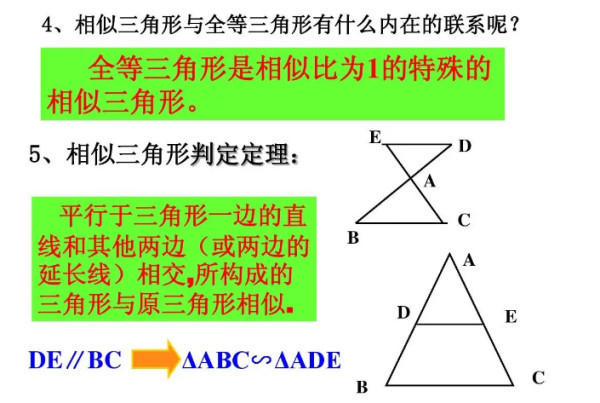
相似三角形判定定理 数学定理 搜狗百科

初中数学沪科版九年级上册22 2 相似三角形的判定第2课时课后测评 教习网 试卷下载

相似三角形的判定 巩固练习 基础 带答案 Doc 悦读文库

三角形相似性复习 文章 三角形相似的定义 可汗学院

解读相似三角形经典图形 参考网

相似三角形的判定

相似三角形 快懂百科

1

27 2 1 相似三角形的判定 人教版九年级下册数学电子课本 数九网

对于两个相似三角形 如果沿周界按对应点顺序环绕的方向相同 那么称这两个三角形互为顺相似 如果沿周界按对应点顺序环绕的方向相反 那么称这两个三角形互为逆 相似 例如 如图 Abc A B C 且沿周界abca与a B C A 环绕的方向相同 因此 Abc 与 A B C 互为顺相似 如图

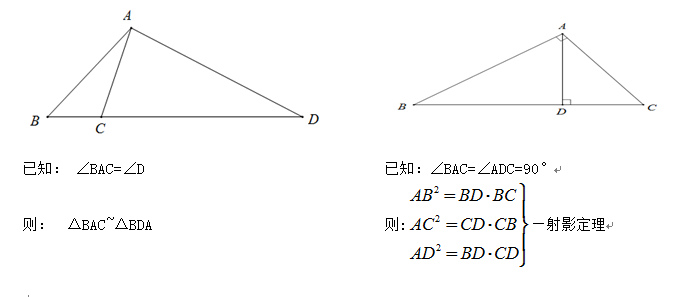
初中数学知识点相似三角形的判定及性质

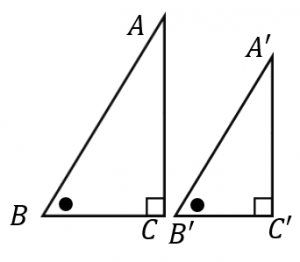
直角三角形の相似条件 具体例で学ぶ数学

相似条件 百度百科

初中数学知识点相似三角形的判定及性质

1

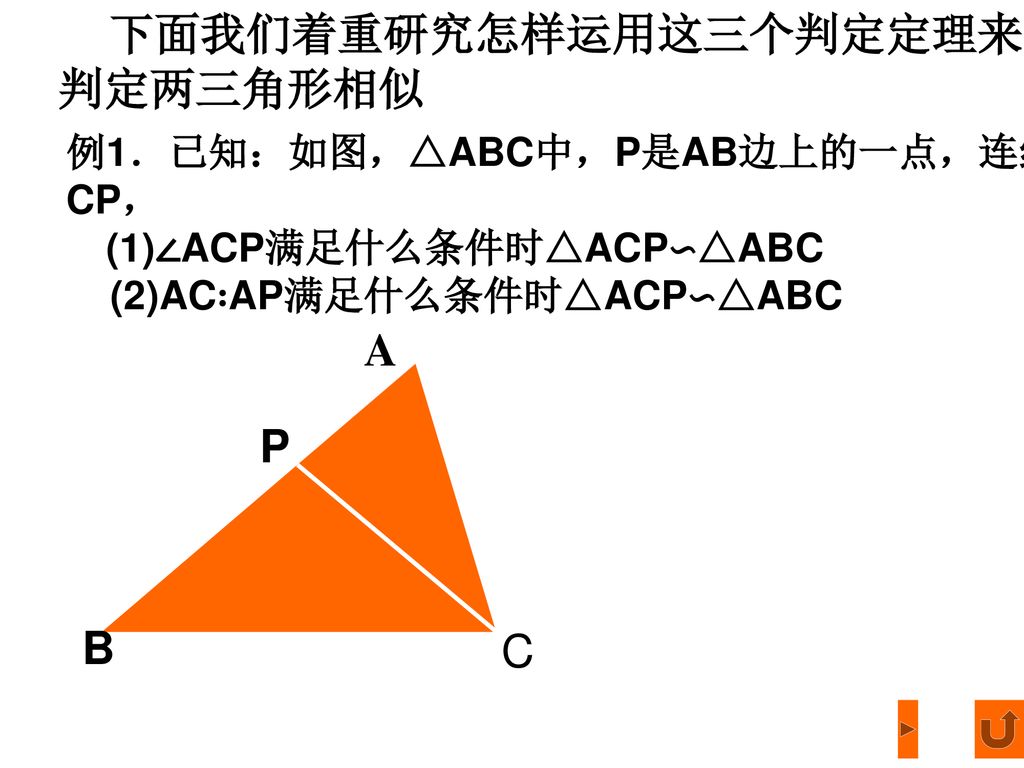
23 3 相似三角形相似三角形的判定 Ppt Download

探索三角形相似的条件 1 云猫文库

数学 中3 44 三角形の相似条件 Youtube

4 5相似三角形判定定理的证明课件 七七文库www 77wenku Com

初中数学4 探索三角形相似的条件图片ppt课件 教习网 课件下载

三角形相似条件 证明 Doc 皮匠网

三相似三角形的判定及性质 人教版高中选修4 1数学电子课本 数九网

探索三角形相似的条件 2 Ppt 教育文库 教育资源网 新时代文库www Xsdwk Com

Ppt 相似三角形的判定powerpoint Presentation Free Download Id

三角形相似条件 シモネタ

中二級10 3相似三角形的證明筆記 哔哩哔哩 つロ干杯 Bilibili

相似三角形中考题汇编19在线阅读

三角形の相似条件 イ弋マ本ゼミナール

初中数学沪科版九年级上册22 2 相似三角形的判定第2课时课后测评 教习网 试卷下载

相似三角形初中数学教案 初中数学教案 中国教育资源网

12 演繹推理幾何 相似三角形 齊齊溫

Download 三角形の相似条件 Images For Free

Conditions For Similarity Of Triangles 3 相似三角形的判別條件 3 Geogebra

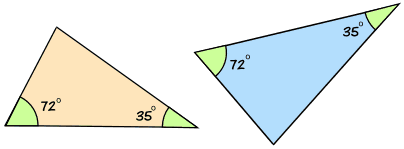
相似三角形的判定

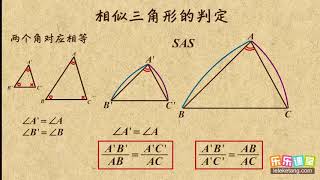
03相似三角形的判定图形的相似初中数学初三 Youtube

判断两个直角三角形相似的条件 网圈部落

平面几何 三角形全等相似模型 一线三等角 K字模型 哔哩哔哩 Bilibili

全等三角形 维基百科 自由的百科全书

相似三角形判定定理 百度百科

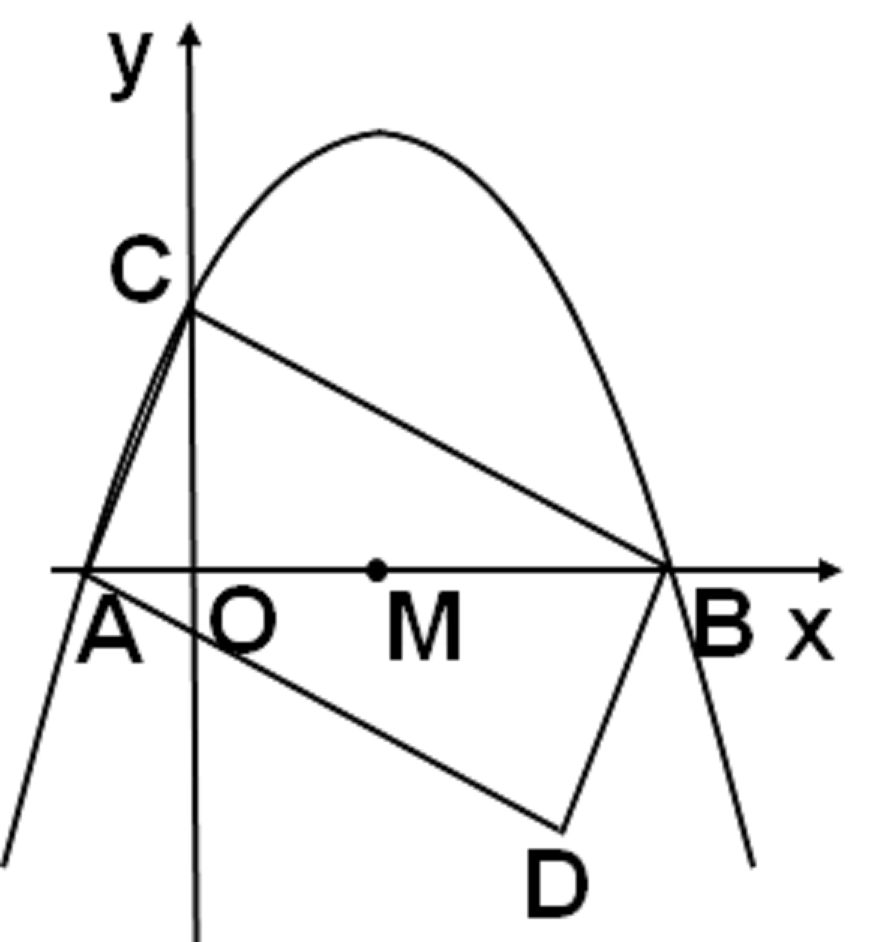
中考数学出题人意图不明时 该怎么办 相似三角形存在性顶点模糊 四边形 问题 矩形

三角形相似的条件 相似三角形对应边成比例怎么证明22已更新 今日 更新 龙飞凤舞诗词网

探索三角形相似的条件 相似图形ppt课件2下载 牛二ppt

三角形相似条件 证明 Doc 皮匠网

相似三角形基础练习题 Doc 悦读文库

觀念 三角形的相似性質 Youtube

判断两个直角三角形相似的条件 网圈部落

探索三角形相似的条件 相似图形ppt课件下载 牛二ppt

第4章图形的相似4探索三角形相似的条件第2课时相似三角形的判定 Ppt 师客文库

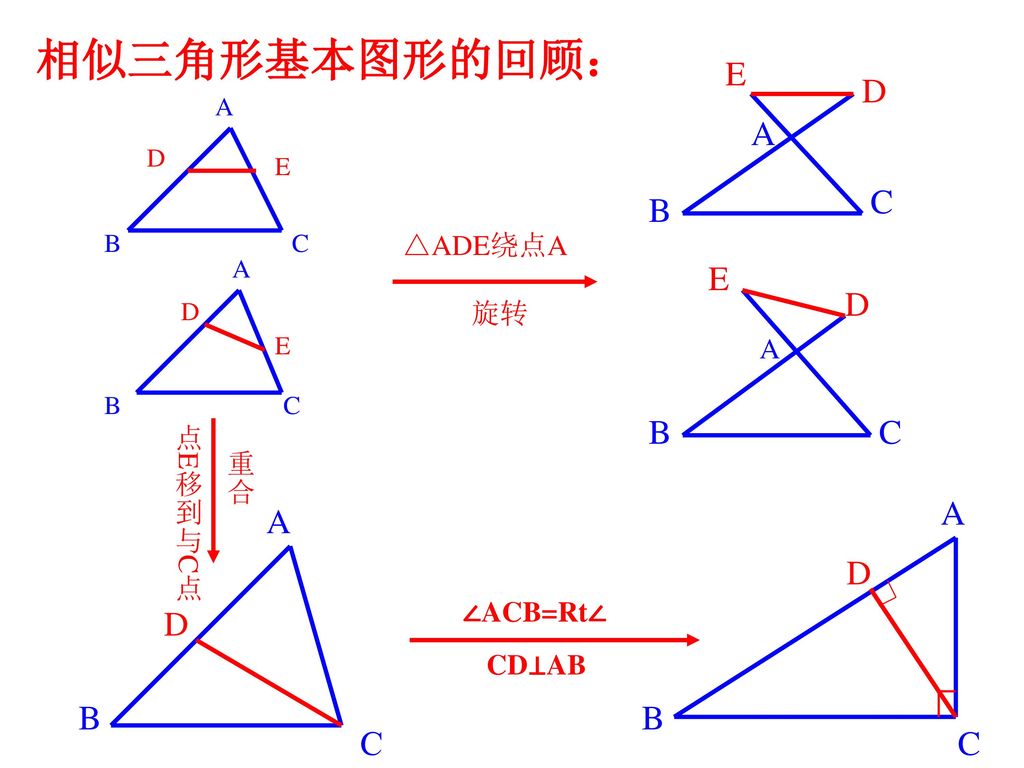
第四章相似三角形复习课 Ppt Download

相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt

第4章图形的相似4探索三角形相似的条件第2课时相似三角形的判定 Ppt 师客文库

三角形の相似条件 Youtube

直角三角形の相似条件 具体例で学ぶ数学

相似三角形的 基本图形 最齐全分类 职场达人网 职场知识 职场礼仪 职场法则

第4章图形的相似4探索三角形相似的条件第2课时相似三角形的判定 Ppt 师客文库

判定三角形全等的思路方法 比较各定理适用条件 更好的应用解题 壹读

教学反思 为什么判定相似不能用 边边角 三角形

تويتر 三角形の相似条件bot على تويتر 三角形だょ

Ppt 相似三角形的判定powerpoint Presentation Free Download Id

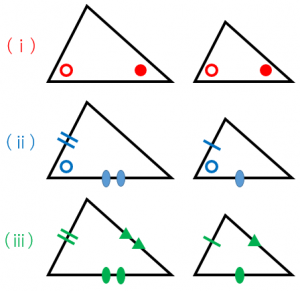
三角形の相似条件と有名な例題３問 具体例で学ぶ数学

试题 19 6相似三角形的性质 Doc 19 6相似三角形的性质 初中京教版13版 数学中国网 Mathschina Com

1

初中数学经典相似三角形练习题 附参考答案 云猫文库

第4章图形的相似4探索三角形相似的条件第1课时相似三角形的判定 Ppt 师客文库

三角形の相似条件と証明問題の解き方 数学fun

Incoming Term: 三角形 相似条件, 三角形相似条件 証明, 三角形 合同 相似 条件, 相似 の 三角形 条件,